FREE LINEAR CUT OPTIMIZER
Information about the optimizer
The linear cut optimizer has the objective of getting near the solution of the less possible left-over. This is achieved by sorting and arranging all the requested cuts. This optimizer is divided in 3 sections. This first one is about introducing all the border conditions that will control the whole operation. In the second section the user must introduce the cutting requirements meaning to fill in all the pieces requested including length and quantity. Finally, the third section shows all the results of the optimization operation together with general information about the run.
1. Configuration
In the configuration section, general values associated to the cutting operation and the losses of the process are requested. In opposition if the values of: losses, saw blade width, variability of the bars and end-cut by side are established in 0, the calculations are done in a ideal frame (a bit fictitious). Following the main configurations will be described in order to have an overview of the impact on the system.
- Bar Length: This is the total length of the stock bars in mm. Max: 20000mm
- Saw blade width: Is the width in mm of the material removed (lost) by the action of the cutting element. Max:50mm
- End Cut (each side): It can be applied in case of having some kind of imperfection on the extreme of the raw material bars. In this way it can be established an amount of mm to be thrown away. The introduced value will be cut in each extreme of the bar, in case it is needed only in one extreme, the value should be divided by 2. This value should not include any other loss or the effect of the saw blade, it remains independent of those. Max: 500mm
- Variability of the bar length: This parameter is useful in case a fix value should be subtracted from the stock bars to compensate length variability issues. Usually, the difference from the longest and shortest bar of a set is the more conservative choice. Max: 500mm
- Losses due to cutting: This field is used in case some repetitive kind of loss is applied in each cut such as process variability, inexperience of the operator or perpendicularity issues. Max: 20mm
- Iterations: Amount of times the simulation will run to obtain the optimal cuts. Low values can lead to results very far away from the optimal but speed-up the calculations. Also note that increasing the number of different lengths of cuts requires more iterations. Max:8000
2. Cut Input
In this section the list of cuts should be loaded in the system. This means each requested final piece should be loaded with length and quantity desired. The system will add and subtract all the values of losses and variabilities established in the configuration area. Always load desired final values (nominal length). Max: 20 different lengths.//Max: 100 (qty) pieces for each length //Max: 300 cuts total For example, to build the frame of a door are needed 2 pieces of 2000mm and 2 pieces of 600mm, considering that the saw blade width removes 2mm in each cut and that the operator inexperience removes 1mm in each cut, the following pieces are loaded in the system:
- Length of the cut= Nominal length + Saw blade width + Losses due to cutting
- 2003mm=2000mm+2mm+1mm
- 603mm=600mm+2mm+1mm
| Quantity | Nominal Length | Losses | Cut Length |
|---|---|---|---|
| 2 | 600 | 3 | 603 |
| 2 | 2000 | 3 | 2003 |
It is defined losses as the sum of losses due to cutting and saw blade width.
3. Bar Length
The bar length used in the calculations is affected by the variability of the bars and the end-cut (each side) declared in the configurations section. For example, if to build a frame of a door (the one of the previous example) there is a stock of 6000mm bars, in which because of esthetical reasons 10mm are thrown away to remove damaged areas, and after this a variability of 1mm (such as a tolerance) is found in all of them due to typical measuring errors, the following dimensions are established:
- Available bar for cutting= Original bar length - 2XEnd-Cuts - Variability
- 5979mm=6000mm-(2X10mm)-1mm
Finishing with the example, inside those available 5979mm all the pieces requested should be arranged including the losses. In the particular case of only 1 door, all the pieces requested fit inside only one available bar, and there is also a left-over.
- Left-Over= Available bar for cutting - (Real length #1 X Quantity of length #1) - (Real length #2 X Quantity of length #2) - ... (Real length #N X Quantity of length #N)
- 767mm=5979mmn - (2X603mm) - (2X2003mm)
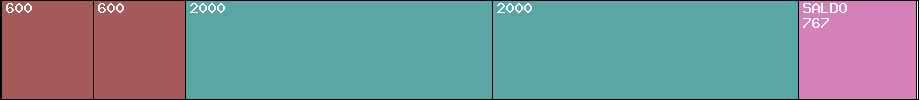
Up to here, everything is simple and intuitive, but in case the necessity climbs to 3 doors instead of only 1, it is not so straightforward to establish the best arrangement of cuts.



And if instead of 3 doors, the new necessity is to build 3 doors + 2 windows of 400mmx200mm, the optimizer starts to come in handy.




4. Working principle
The optimization algorithm is divided in 3 main stages, the first one is about finding possible bars and cut combinations, the second is aimed to select which of these combinations satisfy the initial user request prioritizing the ones with less left-over and the last one is to run the previous results through a post-refinement algorithm.
In this first stage the configured amount of iterations are executed with the aim of obtaining through a montecarlo simulation scheme a set of possible combinations of cuts per bar that are compatible with the initial requests of the user. The random process gathers a huge amount of bars in a very short-time, more iterations are needed if the amount of different lengths grows. By the way this is not a typical montecarlo simulation, just placing random cuts but also takes into account the amount of cuts per bar in order to force incomplete bars that will come handy close to the end of the optimization. This double process consumes more iterations in order to have as many combinations as possible, something very challenging once a small amount of different length is passed.
The second stage performs a sorting and filtering based on an algorithm that penalize the bars with bigger left-over, proposing a very good solution for low-complexity problems (low amount of different lengths)
Finally the results go through a post-refinement algorithm that recalculates all the previous results and optimize them further as a final working set based on some hard-coded parameter.
This leads to having a very good set of solutions for a big amount of daily problems, but is possible that for some arrangements of lengths and quantities (specially for lots of different cuts) and random events the solution reached is not so close to the optimal.
Up to her I haven’t mentioned the graphical and output algorithms, because they are not linked to the optimization core of the software, even though they were very interesting to develop.
5. Warranty
By now I believe the solution is pretty acceptable in the range of lengths and quantities I did my tests, but remains on each user to assess is the solutions are good enough or not. Afterall the computers do the work, but the humans should verify it, for this the graphical output is quite useful.
Under a whole different scenario of infinite resources (time…), mathematically wise I believe it would be interesting/adequate to address this issue from an integer programming approach, even though I haven’t taken that route, because I was not sure enough on how to tackle the scaling of resources while incrementing the amount of different lengths. On the other hand, this development is direct, easy-enough and effective and with not so many steps I was able to put it to work. Said this, I firmly believe it would be interesting, one day, to obtain an alternative based on another optimizing method to compare under daily range of values and mainly assess and compare the speeds or resolution. All the restrictions imposed on the system tend to assure a safety frame of operations for the system, but should be noted that it was tested with values 10 times bigger with very results.
Up to know I don’t record any type of statistics about the kind of cuts or use of the system, but I do not discard doing it in the future to improve the algorithms and aim better the solution and restrictions to the user’s requirements.
Finally I must admit that this small project helped me to remember some concepts operations research and retake some programing routines. Considering everything said, there are not warranties about nothing, but that just makes it more fun. This is life, take risks, have fun.
